Refactoring and Programming Language Semantics

Refactoring improves the design of code without changing its observable behavior. But what is observable behavior? We’ll look at how language semantics affect that. When you devise new refactorings, you have to take semantics into account.

The Simple View is Too Simple

One way to think of a program is like this:

inputs → Program → outputs

The observable behavior is the output it gives in response to the inputs. But we know that many programs deal with randomness, time, threads, other systems, etc., so the outputs are not deterministic.

Furthermore, a program is not just a math theorem – it runs on a real machine. It takes time and space – and we can observe that too.

Language Semantics

Compiler writers face a dilemma similar to that of those who refactor: Given a program, what does it mean? It’s pretty hard to compile a program if you don’t know that!

We need ways to describe meaning of a program by how it works in a domain we understand. One approach is “define how it works in terms of a machine” (and then we have to describe the machine!). Another approach is “define how it works in terms of well-understood mathematics”, and we’ll take that approach.

Let’s look at a few examples of meaning and refactoring.

Simple Expressions

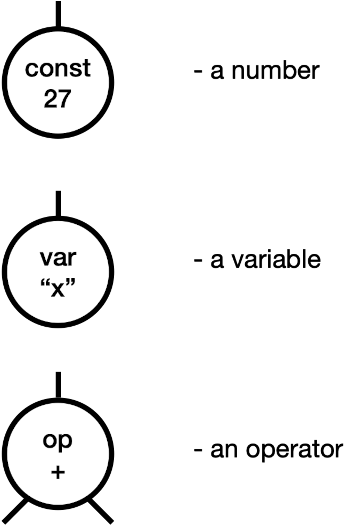
Take simple arithmetic. An expression can take three forms; we’ll ignore parsing, and just work with the tree form.

To define these, we’ll use two functions. “Store” is a dictionary from variable names to integers; “eval” computes the value of an expression using a store.

store: Name → ℕ
eval: Expr → Store → ℕ

The funny N is the symbol for integers, so we’re defining how to move from our programming language (ass trees) to math we already understand.

Here are the rules for evaluation:

Let me wave my hands on the const evaluation, to say that c on the right-hand side is a (math) integer.

Notice also “+” on the left-hand side is part of the program, but the right-hand side “+” is mathematical addition of integers.

Refactoring

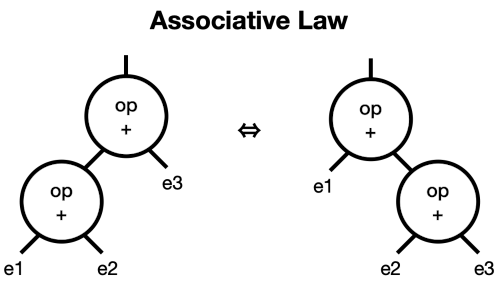
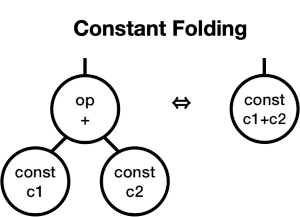
Let’s define three refactorings: the commutative law, the associative law, and constant folding.

The commutative law for addition says we can reverse the order of arguments. We apply our mathematical understanding to a tree transformation:

The associative law says you can add values in any order:

Finally, constant folding lets us combine constants in the tree domain, and captures our intuition that you can replace the sum of two constants with the value of the sum:

You should be able to convince yourself that you can transform the tree for 3+x+4 to x+7, as well as transform it algebraically. In other words, they’re equivalent.

Computer Arithmetic

The semantics above are a starting point – they’re intuitive, but they’re not the full story! Most languages don’t uses true integers, they provide approximations.

For example, a Java int uses 32-bit two’s-complement values. Furthermore, the language definition specifies that overflow and underflow are ignored. An integer is between constants MININT and MAXINT.

This means our definition of addition has to change

eval( e1 + e2, store) = eval(e1, store) +_J eval(e2, store)

where +_J is defined like this:

e1 +J e2 = 
  if e1 + e2 > MAXINT then
    (e1 + e2) - 2 * (MAXINT + 1)
  else if e1 + e2 < MININT then
    (e1 + e2) + 2 * (MAXINT + 1)
  else
    e1 + e2

with “+” and “-” on the right side of “=” being the normal mathematical operations.

How does this affect our three transformations? It doesn’t – since overflow and underflow are ignored, the results are the same before and after transformation – but bounded integers aren’t the same as true integers.

Now Do C

Different languages have different semantics. C does not use Java’s rule that operations resulting in overflow ignore the overflow, but rather “Operations resulting in overflow are undefined.” “Undefined” sounds harmless enough, but it’s not. It means “the system can do anything it wants”. It could ignore it as in Java; it could throw an exception; it could release the kraken.

So this would be a perfectly valid definition:

+C = 
  if (e1 + e2) > MAXINT then
    0   // could be anything! 
  else if (e1 + e2) < MININT then
    42  // or whatever
  else
    e1 + e2

In C, our transformations are no longer universal: they’re valid only if all intermediate computations stay in bounds. If anything could go out of range, the transformations are invalid.

Thus 1 + x – 2 seems like it should be equivalent to x – 1. But what if x = MAXINT or MININT? Then it would stray into undefined territory.

Absolute Value

It looks like Java made a reasonable compromise choice (certainly learning from experience with C). But you can still get in trouble.

Consider the absolute value function:

abs(x) = 
  if x >= 0 then
    x
  else
    -x

From this definition, we expect that the absolute value is 0 or higher.

But, even in Java, that’s not true. Consider the case of MININT. It has the value (-MAXINT – 1). If you negate it (e.g., by calculating 0-x), you’ll find that -MININT = MININT. That is: Math.abs(Integer.MININT) is less than 0!

Key Idea re Language Semantics

Language details matter. The semantics of numbers and expressions may be unexpected, especially in the face of underflow or overflow. Integers are probably the simplest case – floating point numbers are even trickier, and there can be other subtle aspects around variables, naming, access and so. Remember that your refactorings have to be safe for all values, not just typical ones.

Space and Time

It’s common that the semantics ignore issues of space and time. This is mostly reasonable – you don’t want the language to operate differently on a machine with 8 GB or 16GB (or even 1TB).

Consider this Java code

int x = 3;
if (f(x)) {
  System.out.println("OK");
}
:

bool f(Integer i) {
  return i > 0;
}

You probably expect this to print “OK”. And it usually will – except when memory is super-low. Java has a difference between “int” and “Integer”. The latter is a “boxed” type – an object containing an integer rather than a plain integer. The rule when you call “f” is that you should allocate space to box the parameter value, and use it in the method.

If you’re low on memory, the boxing will fail, and calling f will throw an error.

Is it safe to refactor, or not? After all, running out of memory is definitely observable behavior. For example, you might want to inline “f” and change it to use int directly.

I would do this refactoring, unless the code was specifically being used to test that out-of-memory situation. Refactoring is usually to improve the design, and most refactorings don’t have dramatic impact one space or time, so I tend not to worry about it.

Key Idea re Time and Space

Refactorings are usually defined at the language semantics level, ignoring time and space. Don’t be surprised if a refactoring makes code take a different amount of time and space. You can define refactorings that target time and space; these are called “optimizations” in the compiler literature. (See references.)

Conclusion

Language semantics typically abstract away from time and space constraints, defining behavior in terms of a domain we understand. This is the behavior we usually understand refactoring to preserve. But we have to recognize that running applications do take time and space, and that a refactoring may affect these dimensions.

IDEs can’t do every valid transformation, so manual refactorings are also important. When we create refactorings, we need to consider the detailed language semantics, and all possible cases. If you don’t, you can subtly change the observable behavior rather than preserve it.

References

“The Java® Language Specification, Java SE 17 Edition“, James Gosling et al. Retrieved 2021-11-09.

“Refactorings from Writing Efficient Programs“, by Bill Wake. Retrieved 2021-11-10.