Functional languages often have immutable data types – you can’t change an object once you’ve created it, though you can include it as part of other objects. Immutable objects are easier to reason about, and prevent errors where two parts of code think they have exclusive access to change the data. We’ll look at a way to implement queues in an immutable way, using two stacks.
Immutable Stacks
Traditional stack implementations typically use either an array plus an offset to the current top, or a singly-linked list where the pointer to the list points at the top.
From an immutability perspective, an array is not a great since it’s a block of data designed to be read and updated.
A list-based stack is a more natural choice. A stack has two possibilities:
- An empty stack, represented by a null, -or-
- A stack with contents, represented by a reference to a cell containing a value and a “next” reference to the rest of the stack.
(We can speak of pointers or references, but functional languages often hide this.)
To push an object onto the stack, allocate the new cell with data, and point it at the current “top” cell. This doesn’t affect the existing stack. Then change the top to point to the just-allocated cell.
To remove an object, move the top pointer to the “next” pointer in the current cell. This only changes “top”.
We thus have a stack that takes space proportional to the number of items, and takes O(1) time. (O(1) means it uses a fixed maximum number of steps, and never has to loop over its contents.)
Test Code
Here are some Java tests for a new Queue class. The tests treat it as an abstract type, so they should work for any implementation approach we look at.
public class QueueTest {
@Test
public void queue_starts_empty() {
var q = new Queue<>();
assertTrue(q.isEmpty());
}
@Test
public void remove_from_empty_queue_throws_exception() {
var q = new Queue<>();
assertThrows(NoSuchElementException.class, q::remove);
}
@Test
public void add1remove1_then_queue_is_empty() {
var q = new Queue<>();
q.insert("A");
assertFalse(q.isEmpty());
assertEquals(q.remove(), "A");
}
@Test
public void add2remove1_then_queue_not_empty() {
var q = new Queue<>();
q.insert("A");
q.insert("B");
q.remove();
assertFalse(q.isEmpty());
}
@Test
public void add2remove2_then_second_value_returned() {
var q = new Queue<>();
q.insert("A");
q.insert("B");
q.remove();
var item = q.remove();
assertEquals(item, "B");
}
@Test
public void add2remove1_add1_remove2_then_right_values_returned() {
var q = new Queue<>();
q.insert("A");
q.insert("B");
var value1 = q.remove();
var value2 = q.remove();
q.insert("C");
var value3 = q.remove();
assertEquals(value1, "A");
assertEquals(value2, "B");
assertEquals(value3, "C");
}
}
Traditional Queues
Like stacks, queues have two common implementations: an array version and a list version.
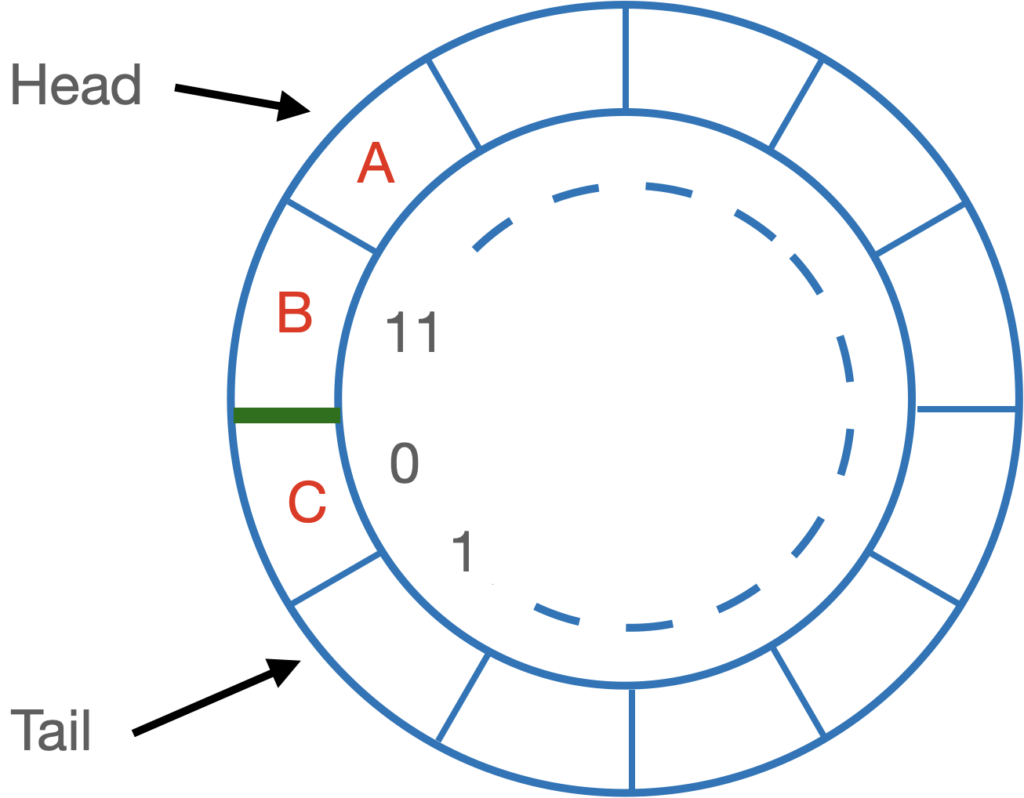
Circular Arrays
The array version says “treat the array as a circular buffer”. This means the head and tail of the list could be in any cell, and that if you increment or decrement a position you must do so modulo the size of the list.
One way is to use two indexes, head and tail. Head is where you remove, tail is where you add. When you want to add an item, put it at the tail position, and increment tail (modulo array size). When you want to remove an item, remove at head – then increment head (modulo array size). (You might consider an alternative: track “head” and “current queue size” instead of “head” and “tail”.)
Here’s an example:
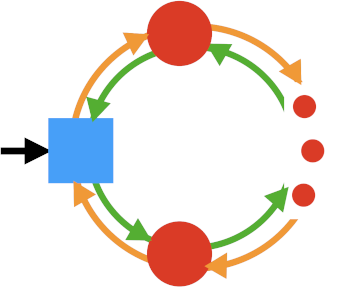
Linked Lists
An alternative is to build a queue from a doubly-linked list. Each cell has a data value, a pointer to the predecessor cell, and a pointer to the successor cell. It’s usually best if you have a “marker” cell that is not part of the list, but is the predecessor of the first cell and successor of the last.
To add to the queue, you allocate a new cell, fill in its data, set its successor to the marker cell, and set its predecessor to the marker cell’s predecessor. Then change the marker’s predecessor to the new cell.
To remove from the front of the queue, take a deep breath, and set the marker’s successor to the marker’s successor’s successor. Then set the marker’s successor’s predecessor to be the marker. I realize that sounds messy. Trace it on a real example and you’ll see why it works. (For a slightly deeper discussion, see “Programming: Using What’s Hidden” in References.)
Both these approaches have flaws from the immutability point of view: we’re either updating an array’s contents, or we’re mucking with pointers in existing cells. Neither is immutable.
Both approaches take O(1) to add or remove, but both use mutability.
Queues from Stacks
We want a queue that works immutably, that takes space proportional to the number of cells in the queue, and that is O(1) to add or remove items. The following two-stack algorithm comes close. (I was inspired by the version in the Haskell book in the References.)
The idea is that you have two stacks: ins and outs. Whenever you add a new item, you add it to the ins stack. Whenever you remove it, you remove it from the outs stack.
Removing is clearly the tricky one – how do objects get to the outs stack for it to be removed? The trick is: if you want to remove, and nothing is in the outs stack, then first pop everything from ins to outs, and then remove from outs.
Here’s an example. Stacks are shown with top at the front; “Ins:Outs” shows the state after each move. (Remove() shows the intermediate steps.)
| Action | Ins : Outs |
| (initially) | _ : _ |
| add “A” | => A : _ |
| add “B” | => BA : _ |
| remove | => _ : AB |
| => _ : B | |
| add “C” | => C : B |
| remove | => C : _ |
| remove | => _ : C |
| => _ : _ |
Code
Here’s an implementation in Java. It uses the Java Stack class which is actually an array-based implementation, but that doesn’t matter to us. We just care that it’s an O(1) stack.
public class Queue<T> {
private Stack<T> ins = new Stack<>();
private Stack<T> outs = new Stack<>();
public boolean isEmpty() {
return ins.isEmpty() && outs.empty();
}
public void insert(T item) {
ins.push(item);
}
public T remove() {
if (isEmpty()) {
throw new NoSuchElementException();
}
if (outs.isEmpty()) {
Queue.emptyStackTo(ins, outs);
}
return outs.pop();
}
private static <T> void emptyStackTo(
Stack<T> ins, Stack<T> outs) {
while (!ins.isEmpty()) {
outs.push(ins.pop());
}
}
}
Analysis
We asked that the queue work immutably. In our code, we hold the two stacks. Those work immutably, so our queue is immutable too.
The size should be proportional to the number of items. The stacks give us that: each piece of data is in one of the two stacks. So the amount of space in use is the sum of the space of the two stacks.
Finally, we want O(1) performance. Stacks give us that for their push() and pop() operations. Our add() just calls a stack operation, so it’s O(1). However, remove() is trickier.
Remove() may have to empty one stack into the other before it calls the stack’s O(1) pop(). But our copy operation might have to copy a whole pile of data at some point. This copy is proportional to the space in use – we call that O(n) where n stands for the number of items. That makes our operation O(n). Bummer.
But all is not lost. Consider how each item is touched: it’s pushed into the ins stack, and later it’s popped from the ins stack and pushed to the outs stack, and still later it’s popped from the outs stack. Nothing ever moves from outs back to ins, so there are no other actions happening to an item.
Thus, every item gets four stack operations. Each of those is O(1), and four of them is also O(1) as it’s a fixed cost per item. In effect, we’re saying that for n items, each will take a constant amount of time, so on average each operation is O(1).
This is sometimes called the amortized cost, the overhead spread over each item. While a worst-case remove() might have to wait while the stack gets emptied, overall the amortized cost is O(1).
Conclusion: What’s Interesting?
I found this algorithm interesting on a few levels:
- I liked seeing a queue implemented in a different way, without an array or a tricky linked list.
- It’s interesting to see how immutability changes data structures. As we use more functional languages, and more multi-threaded systems, techniques like this will be more important. (See Okasaki in References).
- This is a good example of an amortized time bound. (And that makes me wonder if we can lower that O(n) somehow.)
References
Haskell: The Craft of Functional Programming, by Simon Thompson. 2011. (I have 2/e but I assume the discussion of queues and other abstract data types is still there.)
“Programming: Using What’s Hidden”, by Bill Wake. Retrieved 2021-11-14.
Purely Functional Data Structures, by Chris Okasaki. 1999. (I read this a while ago; I think more would have “stuck” if I’d implemented instead of just reading:)