Test-Driven Development (TDD) depends on assembling well-tested parts into a trustworthy whole. Some design structures make this easier. Today, we’ll look at trees.
A tree is a structure consisting of leaf and interior nodes. An interior node contains some number of sub-trees. A tree has a single root node at the top; all are other nodes are its descendants. These nodes may contain information (possibly different information for different types of nodes); they may be mutable or not.
Trees are the basic model for any hierarchical structure.
Information Flow
One of the things that makes trees attractive is that we can traverse them in well-understood ways.
The two most basic traversals are upward and downward.
An upward traversal can let the value of a node be a function of its children. A downward traversal can let the value of a node be a function of its parent.
Example: Upward Flow
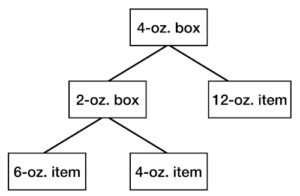
Suppose we want to compute the total weight of a package, where a package contains items or other packages.
An item’s weight is a known quantity. A package’s weight is the sum of the things it contains, plus its box weight.
So, to calculate the total weight of a package, we can do an upward traversal, working from the leaves to the root.
Here’s a Swift implementation. It uses “indirect enum”, which builds a tree recursively.
indirect enum Package {
case item(_ weight: Int)
case boxed(_ boxWeight: Int, _ contents: [Package])
var totalWeight: Int {
switch self {
case .item(let weight):
return weight
case .boxed(let boxWeight, let contents):
var result = boxWeight
for item in contents {
result += item.totalWeight
}
return result
}
}
}
The second case reflects the bottom-up approach – we can’t calculate the total weight for a package until we’ve calculated the weights of everything it contains.
Example: Downward Flow
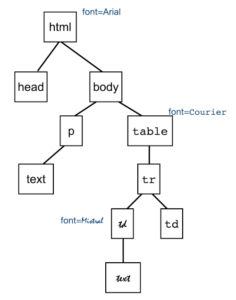
Consider the tree for an HTML document and how styles get assigned to nodes: they flow from the root toward the leaves. If a node sets a new style (e.g., directly or via CSS), it applies to that node and its descendants, unless one of them sets a new style.
In the tree shown, the font is Arial, except for nodes from the TABLE down where it’s Courier – except for its first TD, which is Mistral (as is its child.)
Notice how each parent passes information to its children but doesn’t get anything from them.
Tree Traversal
Trees have several standard traversal, approaches to walking the whole tree node by node.
The most common are postfix, infix, and prefix. They work left to right, but you could clearly make analogs that work right to left instead.
Postfix (post-order): Visit subtrees from left to right, then visit the root. Our “downward flow” example used a postfix traversal.
Infix (in-order) [usually for binary trees]: Visit the left child, then the root, then the right child.
Prefix (pre-order): Visit the root, then visit the subtrees from left to right. Our “upward flow” example used the prefix traversal.
Checkpoint: A Stable Approach
What we’ve described so far is a stable design: information flows in one direction only (either up or down). There is no circularity. The result is easily understood: either parent values are a function of the children’s, or children’s values are a function of their parents.
Computations are local. Each node does its own work; its children may have to do more, but that’s not this node’s problem.
The structure is familiar, too: we’re used to trees, hierarchies, and outlines even outside the software context.
Many applications need nothing more than this; it’s straightforward to implement (once you understand recursion), easy to understand, and stable. Stop here if you can!
Simple flows aren’t enough for some applications; we’ll look at those next.
Complex Flows and Traversals in Trees
What if you can’t get the information you need in one pass up or down? A more complicated approach can make this work.
If we can do what we need in a fixed number of traversals, we retain stability: the answer will converge without risk of running forever.
However, if the number of traversals depends on the content, the system may be unstable, e.g., flickering back and forth between two results.
We’ll look at a couple examples where a more complicated traversal is needed.
Example: Up Once, Down Once
Suppose we’re building a compile for a programming language where constants and variables are typed either integer or float. Some constants are clearly float (e.g., 3.2), others could be either (e.g., 42).
Suppose we have overloaded operators (+, *, etc.) that can work with either type. They require both operands to have the matching types. (Mismatched types would need to use a conversion operator.)
Given an expression as a tree, our job is to label every node as float or int, or flag an error.
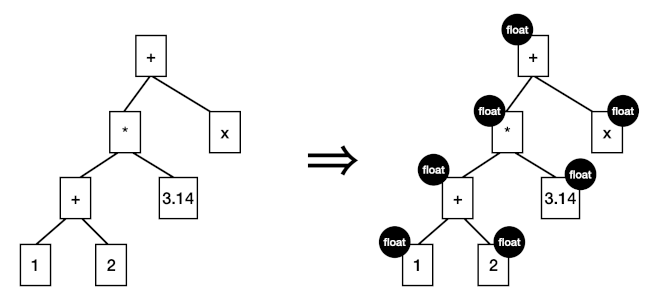
We’ll use a 1-up/1-down traversal strategy.
On the upward calculation, calculate the type of each node to be int, float, either, or error, by these rules:
float variable => float
int variable => int
float constant => float
int constant => either
For operators, use this table for “a op b”:
| a \ b | float | int | either | error |
| float | float | error | float | error |
| int | error | int | int | error |
| either | float | int | either | error |
| error | error | error | error | error |
The upward pass will set many values, but will leave some typed as “either”. For example 2+3 has the value “either”, until we find out if this sub-expression will combine with an int or a float.
If the root node is “either”, set it to int. Then make a downward pass, passing the parent’s type (the target) to the child. Each node uses this rule:
if my type == "either" {
set my type to the target
} else {
leave my type alone
}
tell each of my children to apply the rule, using my type as the target.
TBD – validate these rules – can new errors happen?
Left-Context Traversal
Some traversals can pass information both up and down, working in a single pass. This works when nodes’ values depend on nodes to its left (what I’ve called “left-context”).
On example comes from compilers: some languages require declaration before use, so the left context contains a variable’s type definition.
But left context has uses outside the compiler domain. For example, suppose we want to number nodes at each level: the root is 1; its first child is 1, its second child is 2; its first grand-child is 1, its second is 2, etc.
To figure out these numbers, we could do a pre-order walk, getting information from the parent about the last index at each preceding node, and passing back revised information as its children are numbered.
I’m not going to go further on this example. Hopefully that sketch is enough to convince you that it will converge on the right answer, and also that you want to avoid that complexity if you can:)
Are There Limits to Trees?
Absolutely. A tree can’t directly represent sharing. It can’t represent arbitrary graphs, or many other structures.
For example, consider this expression:
a[r * cols + c] = 1 - a[r * cols + c]
A tree represents r*cols+c twice, but we’d like to avoid recomputing it. To capture this commonality, we need some structure other than simple trees.
Conclusion
A tree represents many types of hierarchies. By using simple traversals, we can be sure algorithms will terminate.
A tree is rarely the whole top-level design, but it’s easy to work with in the parts that can use it.
Bibliography
Compilers: Principles, Techniques, and Tools (2/e). Aho, Lam, et al. Addison-Wesley, 2006. ISBN 978-0321486813.
“Tree (data structure)”, Wikipedia. https://en.wikipedia.org/wiki/Tree_(data_structure). Retrieved 2024-04-21.
“Tree traversal”, Wikipedia. https://en.wikipedia.org/wiki/Tree_traversal. Retrieved 2024-04-21.