When you have hierarchical information, a tree is a natural representation. We’ll look at ways to test-drive trees and their close variants.
Trees
A tree consists of nodes which may have child nodes. The nodes form a hierarchy – no loops or disconnected nodes. A node’s children may be a set (unordered) or a list (ordered).
A node may be restricted to having 0, 1, or 2 children, in which case it’s a binary tree.
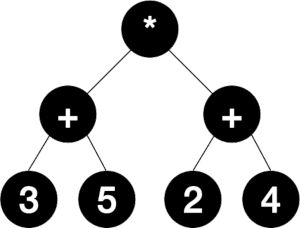
Example – Arithmetic Expression: (3+5) * (2+4)
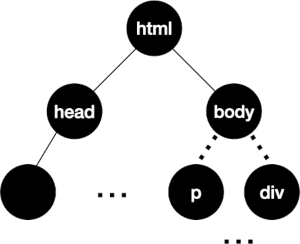
Example – HTML: <html> <head> ... </head>...</html>
Tree Implementations
A very common representation of a tree is as node objects, containing a list of (pointers to) its children. The nodes may all have the same type, may share a parent type, or may be different types. Nodes usually have information attached. Sometimes, each node has a pointer to its parent as well.
Some trees maintain extra “bookkeeping” information to help the tree be self-balancing. This makes common operations on a tree of n nodes be closer to O(log n) performance than O(n). Some examples include red-black trees, B-trees, and AVL trees. (See “Self-balancing binary tree” in the References.)
A heap stores a binary tree as an array with the root at position 0, and the children of node i at positions 2*i+1 and 2*i+2.
Design Patterns
Several design patterns are tree-related. (See References.)
- Chain of Responsibility – passes responsibility up a tree-like structure.
- Composite – defines a tree structure.
- Interpreter – assigns meaning to a tree.
- Visitor – defines ways of walking through a tree, with objects that know how to handle each node type.
Tree-Like Objects
Tree-like objects share characteristics with trees but are not typical trees. Some examples:
Forest
A forest is a set of trees, with no single root. You may represent it as a set, or you may find it handy to create an imaginary root, holding the root nodes of the trees.
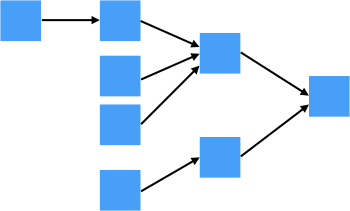
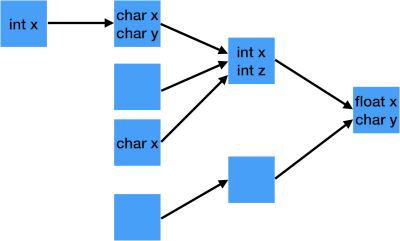
Directed Acyclic Graph (DAG)
A directed acyclic graph is a directed graph with no loops (cycles). The nodes in a DAG point to their children, and you’re allowed to re-use (share) child pointers. (DAGs also have the potential of having multiple roots.)
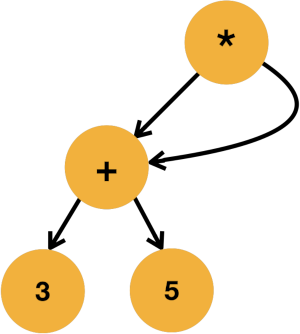
For example, a compiler might represent (3+5)*(3+5) like this:
The shared subtree can help the compiler generate code that only calculates (3+4) once.
Mind Map
Mind maps are typically represented as a hierarchy (root in the center), plus cross-links that connect arbitrary nodes.
Chain of Responsibility
A chain of responsibility sets up a delegation strategy: a child handles something if it can, or passes it to its parent for handling if not. I think of it as tree-like because the parent relationship is represented, but the child relationship is usually not.
Symbol Table in a Compiler
The hierarchy represents textual nesting, with outermost scope to the right. They may be connected like a chain of responsibility, or have links both ways.
Non-Uniform Nodes
Non-uniform nodes are trees, but their handling gets complicated when there is no common type. Traversing it may require custom code at each level, rather than a single navigation that all nodes understand.
For example: Series – Book – Chapter – Text
Test-Driving Tree-Like Objects
Sufficient completeness
As for list-like objects (see References), consider the various ways to build and modify an object, and ensure each observer method is well defined for each case.
With trees that reorganize themselves, you need to take extra care to cover all possible configurations. Two trees containing the same values may have different structure depending on the order of operations that created them.
How you will build the tree, all at once, or incrementally?
Invariants
As with list-like objects, there are often cases where the tree maintains invariants that aren’t observable through the public interface. This is especially common with trees designed to optimize performance – their public interface may be that of a simple tree, but there’s extra work behind the scenes.
For example, consider a heap that always has the smallest value at the root. When a new value is added, the heap must be adjusted to restore its invariant – that each node is >= its parent.
Top-Down or Bottom-Up?
Some things are calculated bottom-up, e.g., the weight of an interior node is the sum of the weights of its children.
Other things are top-down. For example, a document has a default font but it can be overridden at the section, paragraph, or character level.
Some applications go both and up and down: a compiler might identify data types bottom-up, then force children to a common type working top-down.
Recursion
Recursion is usually the easiest way to process trees. The challenge with recursion is that it may blow up if the tree is too deep.
I’ve seen a few techniques to deal with this:
- Recursive methods can have a parameter for the depth, and refuse to go too deep. (Typically the public interface calls a helper method with an extra parameter.)
- Convert recursion to iteration, perhaps with the help of an explicit (bounded) stack.
- Use an algorithm that modifies the tree in place, to embed navigation cues. (See “threaded trees” in Knuth, in References.)
Testing Order
It’s generally easiest to work from a one-layer tree (leaf only) up to full trees.
Begin by testing one or more types of leaves. Then test combinations for each type of intermediate node. By the end, you need to test all leaf and interior nodes.
Consider the arithmetic tree at the start: (3+5)*(2+4). These would probably be my tests:
- Single integer node – 3
- Plus node – 3+5
- Multiply node – 2*7
- A multi-level “acceptance” test, expected to pass: (3+5)*(2+4)
Some behaviors depend on the width. Again, work from small to large: narrow to wider.
Walking a Tree
You often need to iterate through all the nodes of a tree. This can be customized for each traversing function. Or, you may pull out a common method to do the walking, passing in a function to do the per-node work. This can grow to a Visitor pattern if you’re walking for different reasons.
There are three common tree-walking patterns:
Prefix: Visit the root, then the left child, then the right child.
Infix: Left, root, right
Postfix: Left, right, root
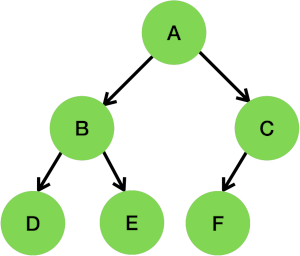
Example: For this tree:
Prefix – Root-left-right – ABDECF
Infix – Left-root-right – DBEAFC
Postfix – Left-right-root – DEBFCA
These aren’t the only options; there are other patterns, such as bounded cutoff (only going so deep) or opportunistic (best candidate first).
Conclusion
Tree-like structures are a great fit for hierarchical information. You’ll generally find it easiest to drive out the tree by working from leaves to small trees to bigger ones. As with lists, it pays to consider how each observer method applies to any possible tree. Finally, there are many ways to walk a tree; find an approach that works for your situation.
References
Design Patterns: Elements of Reusable Object-Oriented Software, by Erich Gamma et al.
“Directed acyclic graph”, https://en.wikipedia.org/wiki/Directed_acyclic_graph . Retrieved 2021-03-22.
Fundamental Algorithms, vol. 1 of The Art of Computer Programming, by D. E. Knuth. Lots of good material on trees and tree-like objects.
“List-Like Objects – TDD Patterns”, by Bill Wake.
“Self-balancing binary search tree”, https://en.wikipedia.org/wiki/Self-balancing_binary_search_tree . Retrieved 2021-03-22.
“Tree (data structure)”, https://en.wikipedia.org/wiki/Tree_(data_structure) . Retrieved 2021-03-22.