State Machines, Part 2: Interpreter Code

In Part 1, we looked at state machines and some common variants. This time we’ll look at code: how can you implement state machines? We’ll look at several approaches, in two classes: interpreter and direct-coded. (You could think “interpreter vs compiler” and not be too far off.)

In the interpreted case (this article), you put your state machine into a data structure, and then use an interpreter that works its way through the data structure. It’s generic in that the interpreter has the same code regardless of the state machine.

In the direct-coded approach (next article), you write code that performs the steps, using commands in the programming language to move between states. In the direct-coded approach, the code is customized to the particular state machine.

Whatever your general approach, there are generally still lots of choices to make about how to implement things. For state machines that are intended to terminate, I’ve assumed there’s a “done” event at the end of the event stream.

Series

• State Machines, Part 1: Principles
• State Machines, Part 2: Interpreter Code [this article]
• State Machines, Part 3: Direct Code
• State Machines, Part 4: Testing

---

Example

We’ll use this example for our interpreters. It’s a specification for numbers, which have digits, optionally followed by dot and more digits. (There must be at least one digit before and one digit after the dot if there is a dot.)

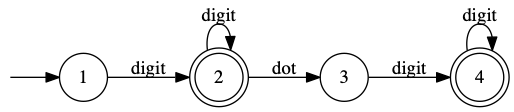
Interpeter

State machines are an augmented graph, so one way to model them is embed the graph part in a typical graph representation, and add support for the extra bits.

Transition Matrix

In this approach, you represent the graph part as a big matrix, labeling the left column with states, and events across the top. The combination of state and event tells you which state to go to next. We’ll use 0 as the error state, and make unused state-event combinations go there.

Here, the first 3 columns show the transition table, and the last column tells whether the state is final.

Event > v State	digit	dot		isFinal[]
1	2	0		F
2	2	3		T
3	4	0		F
4	4	0		T

You need another structure too, to indicate which states are end states. This could be a set of states, a map of state to boolean, etc. We’ll assume a table isFinal[], indexed by states.

To add behavior when you enter a node, you can have another table mapping from state number to an action. If you want behavior when traversing an edge, you can either put state+action in the cell, or have a parallel table.

The interpreter looks something like this:

state = initialState
while true {
  event = nextEvent()
  if transition[state][event] != 0 {
    state = transition[state][event]
  } else if isFinal[state] {
    return state
  } else {
    return 0
  }
}

Optimization: You may have a matrix that is large but sparse (mostly zeroes), and/or you may have a lot of duplication (similar rows or columns). You can apply any valid compression techniques (provided they don’t change the effect).

For example, if you’re doing a token recognizer for a programming language, you may find that A-Z and a-z are treated identically, and that rather than working directly off characters, you can define your events as character classes to reduce the number of columns substantially.

Critique: The nice thing about this approach is that you write a single interpreter that handles any state machine. You do have to worry about table size. For example, some compilers have many thousands of possible events (one for each Unicode character). If you have actions for states or transitions, it can be hard to understand how they fit together.

Node and Edge Objects

Another way to represent a graph is to have a Node class that contains a set of edges. In the case of a state machine, the set is really an “event to node” map.

  public class Node {
    bool isFinal
    Map<Event, Node> edges
  }

This is almost a direct translation of the picture we used above; here it is again to help you trace the interpreter algorithm.

The interpreter is similar to the earlier one:

state = initialState  // a Node
while true {
  event = nextEvent()
  if state.edges.containsKey(event) {
    state = state.edges[event]
  } else if state.isFinal {
    return state
  } else {
    return STATE_ERROR   // a pre-defined node
  }
}

Critique: For a sparse state machine, this saves space compared to the other approach (since we don’t have to have entries for error states). It’s a bit more work to set up. In many languages, you’d have to set this up at runtime, so that creates issues around how you’ll get the data to create the graph.

Direct-Code Approaches

In the next article, we’ll look at ways of encoding the state machine directly into code. However, before we leave, we’ll look at probably the most common approach: implicit and ad-hoc.

Implicit and Ad Hoc

Many programs have an implicit state machine: it’s in the code but you have to infer its existence. And the state machine is usually ad hoc: not created or used in a systematic way.

I took this approach in a Yacht dice game I implemented a while back. Compare the code the diagram below; they’re functionally equivalent but you definitely wouldn’t say either one defines the other. (That’s one way it’s ad hoc: some things that could be done with the state machine are done as other code, according to the author’s whim, not reflected in the diagram.)

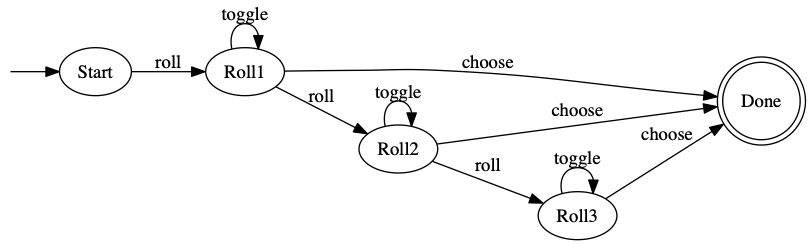
In the code, the state is represented as a combination of values: canSelectDice, rollsRemaining, canRoll, and canSelectCategory. (Notice how they’re part of a class that manages several other values too.)

This class isn’t the whole story, though. The dice selection (for re-roll) seems to be partly here and partly somewhere else. (In reality – since toggling never changes the state, the state-oriented code basically ignores it. But canSelectDice is tracked and used, since you can’t toggle until you’ve made your first roll.)

Code from the Yacht Game

public class Game : ObservableObject {
  let rollsPerTurn = 3
  let numberOfDice : Int

  @Published var hand: Hand
  @Published var scoreCard: ScoreCard

  @Published var canSelectDice: Bool
  @Published var rollsRemaining: Int
  @Published var canRoll: Bool
  @Published var canSelectCategory: Bool

  @Published var shouldReplace: [Bool]
  @Published var totalScore: Int = 0

  var randomNumbers: () -> Int
  var cancellables = [AnyCancellable]()

  public init(numberOfDice: Int, diceCup: @escaping () -> Int) {
    self.numberOfDice = numberOfDice
    // ... initialization omitted

    // Start game:
    rollsRemaining = rollsPerTurn
    canRoll = true
    canSelectDice = false
    canSelectCategory = false
    shouldReplace = Array(repeating: true, count: numberOfDice)
  }
  
  fileprivate func rollWasMade() {
    rollsRemaining -= 1
    canRoll = rollsRemaining > 0
    canSelectDice = canRoll
    canSelectCategory = true
    shouldReplace = Array(repeating: false, count: numberOfDice)
  }

  fileprivate func categoryWasSelected() {
    rollsRemaining = 3
    canRoll = true
    canSelectDice = false
    canSelectCategory = false
    shouldReplace = Array(repeating: true, count: numberOfDice)
  }

  public func roll() {
    objectWillChange.send()
    hand.roll(replacing:shouldReplace)
    rollWasMade()
  }

  public func select(category: Category) {
    objectWillChange.send()

    scoreCard.choose(category: category, hand: hand)
    totalScore = scoreCard.score()
    canSelectCategory = false
    canRoll = true

    categoryWasSelected()
  }
}

Now, this implicit state machine is admittedly very small, but already a state machine might clarify things. And if you add new rules or requirements (such as “you can’t re-roll unless you have something toggled or “start a new game when the old one finishes”), a more explicit state machine could become more valuable.

Conclusion

We looked at a couple interpreter-based approaches to building a state machine. They have similar code but different memory needs.

In general, interpreters have a reputation for being slow, but it’s hard to know without measuring. For example, the interpreter is a small loop that may fit in an instruction cache much more easily than direct code that goes on and on. (As always – measure!)

Interpreters have another nice property: you can define different meanings of “interpret”. For example, for testing purposes I might like an interpreter that remembers which states or transitions were used. For analysis purposes I might want to see characteristics of the states, or of paths involving them. It’s much easier to work these into the interpreter structure than do the corresponding things in direct code.

It’s all a tradeoff, of course.

References

“State-transition table”, https://en.wikipedia.org/wiki/State-transition_table, retrieved 2020-10-19.

---