Sets are fundamental in mathematics — and programming. We’ll look at some considerations when using Test-Driven Development (TDD) for set-like objects.
This is the last in a series of articles describing TDD for container objects; see the References for the others.
The Jobs of a Set
Sets provide several common operations (see References):
Membership Testing – determine whether something is in, or not in, a set.
Iteration – deliver the members of a set one at a time.
Set Algebra Operations – form the union, intersection, complement, etc.
Representations
A fundamental idea like “set” has many possible representations:
Bit String
For sets with a small range, a string of bits can represent the set. For example, if values have the range 0..63, a 64-bit unsigned integer can have the corresponding bit set. For a moderate range, with approximately equal likelihood of being in or out, operations tend to be very quick. In the best case, they’re simple hardware-level instructions like “and”, “or”, “xor”, or bit shift.
List
Store the items of a set in a list. You must preserve the constraint (or the illusion) that each item is only stored once.
With lists, operations are often O(n) – proportional to the length of the list. Some linked-list approaches move the most recently accessed item to the front, which can speed up some operations. Variations such as the skip list (see References) attempt to average O(log n) performance.
Hash Table
By defining a function that maps any element to a number, you can store items in a (typically) sparse array of values. You can do a lookup in O(1) on average.
Tree
By storing elements in trees, you may be able to get O(log n) access. In general, this requires self-balancing structures such as red-black trees.
Etc.
Just about any container type can be used for sets: heaps, tries, arrays, and so on.
Set-Like Objects
Set-like objects share some characteristics or operations with sets, but also have differences.
Multi-set aka Bag
A multi-set is a set that allows repetition – the same element can be in the set multiple times. For example, think of a wallet containing a ten, and five, and three ones. You care about the denominations and their counts.
Ordered Set
Some applications require a set to iterate in a particular order. If the set can do it, it saves you from having to iterate the items, store them in a structure, sort them, and iterate through the result.
Map
A map (e.g., a hash table) can represent a set (by using an element as a key, and mapping the key to itself or a constant), but it can also represent the mapping (a function) from an element to some other object.
Database
SQL (and other) databases have set behaviors at their core.
Spelling List
One of the early Unix spell implementations (see References) used a one-sided membership test. If the list said “no” then a word definitely was not in the vocabulary list. But if the list said said “yes”, odds are it’s a good word, but it might be misspelled. (The implementation worked by running vocabulary words through multiple hash functions, and storing the results of each. Usually a misspelled word would “miss” at least one hash, but could by chance make it through all of them.)
Symbol Table
In a previous article, we described symbol tables as a tree-like object (see References). But a symbol table also acts like a set, as you retrieve name information, and iterate through the list of names.
Test-Driving Sets
As with lists or trees, sufficient completeness can give you good ideas for driving set-like objects: Identify the ways to build and mutate an object, then verify that each “observer” method behaves as it should.
You also may find invariants helpful – they should start true when the object is built, and remain true after any possible mutation.
With so many varieties of implementations, you may find that you have to focus on specific situations that your algorithm addresses. This is common when an abstract data type has multiple implementations: the public interface makes things sound simple, but the data structure may have special handling for certain situations.
For example, if your representation is a self-balancing tree, you’ll need examples that trigger the self-balancing behavior. It’s common for the sequence of operations to matter: set.add(a).add(b) may have a different representation than set.add(b).add(a). You may need very complex data to trigger all the situations you want.
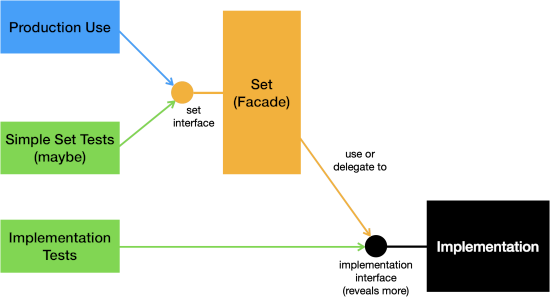
Opening up the Box
When the internal representation varies enough from the public interface, you may need to reveal more to test it thoroughly.
There are two common approaches:
- Expose more information to the test (e.g., with access modifiers).
- Split the class into a public interface that delegates to a specific implementation, and test the implementation directly.
This is like splitting a large class: Your implementation tests benefit from a richer interface, but the “surface area” of the system has grown.
Conclusion
We looked at the basic operations for sets, then several common implementations: bit string, list, map, tree, etc. We considered some set-like objects too: multi-set, ordered set, map, spelling list, database, and symbol table. These are like sets, but have some difference, e.g., in sorting or duplicate handling.
Finally, we talked about using sufficient completeness as a testing pattern: consider all the ways to create and mutate objects, and what that does to “observer” methods.
References
“Development of a Spelling List“, by M. Douglas McIlroy. From IEEE Transactions on Communications, Vol. COM-30, No. 1, January, 1982.
“List-Like Objects – TDD Patterns“, by Bill Wake. Retrieved 2021-03-28.
“Set (abstract data type)“, Wikipedia. Retrieved 2021-03-28.
“Skip list“, Wikipedia. Retrieved 2021-03-28.
“Tree-Like Objects – TDD Patterns“, by Bill Wake. Retrieved 2021-03-28.