Pipelines – Confidence in Design

The other day, Kent Beck pointed out a skill that test-driven development (TDD) relies on but doesn’t give much guidance about: “behavioral composition”. This is the skill of dividing a big behavior in such a way that we trust the whole solution if we trust the parts.

We’ll look at one of my favorite approaches – the pipeline.

The Problem

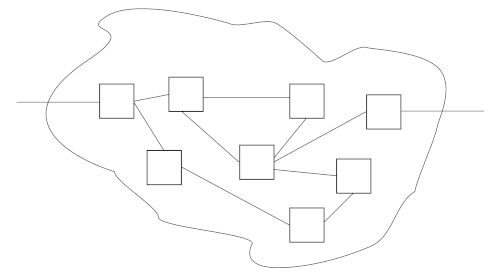
Software solutions may look like this:

Such an approach may work, but it’s hard to have confidence in it. Even if we trust the parts, can we trust the whole?

TDD is good at giving us trust in small components. But as we interconnect them into a larger system, we risk that many scenarios work, but may have hidden dependencies or assumptions that might bring the whole system down.

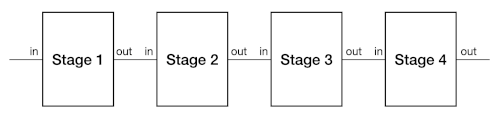
The Pipeline

A pipeline consists of a set of stages, arranged so that the output of one stage feeds into the input of the next. This design structure can give us confidence that the whole really is the sum of its parts.

Note that a pipeline is a linear sequence, with no loops or backtracking.

Pipelines as Functions

We can treat each stage in a pipeline as a function. A function is a rule that defines a consistent output value for each input value. (If any stages aren’t functions – e.g., a random number generator – we’d need a different analysis.)

A pipeline sends a value through the first stage, then sends the result of that through the second stage, and the result of that through the third, and so on till a value comes out the end.

We can notate f: A → B to mean that f takes an argument of type A and produces a value of type B.

Mathematics suggests a way to combine functions, that corresponds to the way we attach pipeline stages: function composition. Given two functions f and g, we can define fog that creates a new function:

(fog)(x) = f(g(x))

To describe a chain of functions, we can apply the operator repeatedly:

(((fog)oh)op)(x) = f(g(h(p(x))))

While this may be accurate, it’s an awkward notation: we apply things from right to left, but at least in English we’re more used to working from left to right.

So, let’s define a new operation ≫ (borrowed from Elm):

f ≫ g = g o f

Function Composition Is Associative

A key rule from mathematics is that function composition is associative. Perhaps you remember the associative law for addition of numbers: (a + b) + c = a + (b + c). Since this is true, we can unambiguously write a + b + c without parentheses.

This works nicely for our notation: stage1 ≫ stage2 ≫ stage3 etc.

Associativity of stages means that we can assemble small pieces of our pipeline and reassemble them into the whole:

stage1 ≫ (stage2 ≫ (stage3 ≫ stage4)) ≫ stage5 ≫ stage6

Thus we can either compose stages linearly or in a hierarchy as long as the result is still a linear pipeline (function). In other words, a smaller pipeline can be treated as a stage.

Next, let’s look at different ways flow can work.

Flow, Element by Element

The simplest flow operates element by element. You might think of it something like this:

for element in input stream {
  result = pipeline(element)
  outputStream.append(result)
}

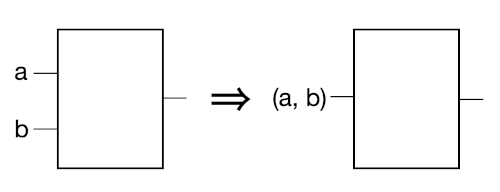
Flow, Multiple Arguments

We’ve defined a stage as taking a single value. If you have multiple arguments, you can wrap them into a single value with a tuple or class.

Flow, By Stream

Not everything can be handled element by element. For example, sorting needs to see all the input before it can tell you the first output. A filter stage may not produce output for every input element (as some get filtered out).

These are still pipelines. The input domains are streams (sequences) rather than single elements.

There are advantages to dealing with the whole stream. For example, Java’s streams can add parallelization with a single function call.

Gaining Confidence

Pipelines can help give us confidence for several reasons:

• The close mapping of pipelines to function composition means that insights from math can give us insights into pipelines.
• Because of associativity, we can split a pipeline into sub-pipelines. We can validate any sub-pipeline as a function converting inputs to outputs.
• Since the interconnection is so simple, most of the testing can focus on the individual stages.
• Because values flow in a straightforward manner, we have clear points we can monitor – where the values go between stages. For example, we could create an “identity” transformation that is a passthrough for values, give it a monitoring capability, and insert it between two stages.
• Values move forward from one stage to the next, never backwards, so the structure is stable. (Backwards flow can create a feedback loop, which can become unstable, as when a mike is too close to the speakers.)
• Pipelines can apply at multiple scales: as a series of function calls, as larger components communicating, as a Unix pipeline, or even across systems connected by a message queue.
• A pipeline has a natural parallelization model: run each stage (or series of stages) in its own thread or process.

Conclusion

A pipeline is like function composition: it combines simple stages (or functions) into a more complex one. Because it is simple in concept, we gain confidence that the whole solution will work if the parts do.

Not every problem easily fits into a simple pipeline, but it’s a great structuring mechanism when it fits.

Even if a pipeline isn’t a total solution, it can still be a useful structuring tool for parts of a bigger solution.

References

“Function composition”, Wikipedia. https://en.wikipedia.org/wiki/Function_composition. Retrieved Apr. 3, 2024.

“The Java 8 Stream API Tutorial”, https://www.baeldung.com/java-8-streams. Retrieved Apr. 3, 2024.

“Pipeline (Unix)”, Wikipedia. https://en.wikipedia.org/wiki/Pipeline_(Unix) . Retrieved Apr. 3, 2024.

“TDD: Test-Driven Development”, https://xp123.com/tdd/. Retrieved Apr. 3, 2024.