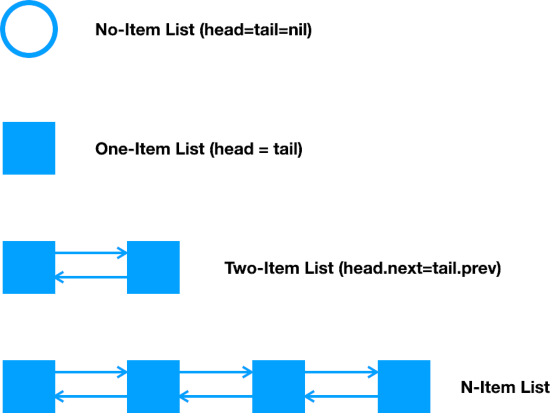
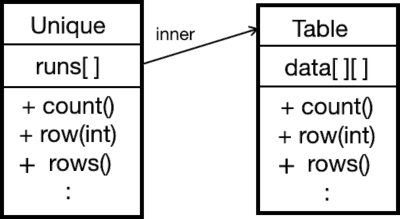List-like objects include linked lists, arrays (somewhat), stacks, queues, deques, heaps, etc. While we can often just pull one from a standard library, other times we have to create our own “linear” types. Let’s look at some tools for test-driving them.
Constructing Lists: Sufficient Completeness
I’ve written about the sufficient completeness approach before (see References), so I’ll just summarize: You can drive tests by considering all the ways to construct and modify the object, then check each accessor against each possible structure form.
In effect, you partition the possible objects into a set of construction forms. This works especially well when those forms are straightforward.
Beginning-Middle-End
For many linear types, the beginning and end of the list are handled specially. This typically affects the first one or two (but possibly more) items. (Empty lists are often a special case too.) The middle of the list tends to work the same for any number of elements.
Case study 1 below provides an example where the beginning and end are critical for one implementation, and much less important for the other. Case study 2 provides an example where the end can be treated like the middle by using a sentinel.
List Properties
Even if you don’t have a property-based testing tool that can generate test cases for you, necessary properties of your object can lock in good behavior as you drive new behavior with tests.
Ideally, you can express these properties in terms of the public interface of the object. Even then, they are often chosen for implementation-specific reasons. That is, while the properties are true of any possible solution, they may be chosen to guard against problems peculiar to your solution.
For example, compare an array-based list with a doubly-linked list. An array is unlikely to have different lists if read front to back or vice versa. But it’s easy to make this mistake with a doubly-linked list. See case study 1.
Here are some properties I’ve found useful:
contents(list-forward) = reverse(contents(list-backward))
list.count <= max -- in a bounded list
count(empty-list) == 0
for any item in list: constraint(item) -- e.g., item > 0
list.count == set(list).count -- if uniqueness is enforced
result is a permutation -- important for sorting
constraints between items, e.g.:
∀ i ∈ 1..count-1: a[i-1] <= a[i] -- for sorting
or
∀ i > 0: a[i] <= a[i/2] -- a heap property
No net effect, e.g.:
stack == stack.pop(stack.push(x))
Case Study 1: Doubly-Linked List
An LRU Cache deletes the least-recently accessed item when it runs out of room. A common implementation is a hash map + a doubly-linked list. (I described this situation earlier, see References – “Programming: Using What’s Hidden”).
My original implementation mostly used the sufficient completeness approach. It had a list like this, with head and tail pointers:
With separate head and tail pointers, and nil on the first and last nodes, there were a lot of cases to consider, including these:
(I think the case that burned me is a different one – a three-item list acts differently than a two-item list.)
After I had implemented it, and was looking it over, I saw an asymmetry in the code. I modified my assertions to not only look for what they expected, but to also check the property “list-forward == reverse(list-backward)”. That revealed that (as suspected) some operations were wrong.
I dredged up memories from a data structures class, and switched to a version using a sentinel node:
I kept the property test, and this implementation turned out much simpler.
It reminded me of a couple things:
- Bugs can sneak in if you don’t have the right tests.
- Knowing better designs produces better code, even with TDD.
Case Study 2: Removing Duplicates
In the data viewer I was working on, when there are duplicate rows, the system displays only one of them and shows a count of the number of duplicates.
In the in-memory version, there’s an underlying table, where rows are numbered from 0. Uniqueness is managed by a decorator that tracks the first index of a run of duplicate entries. (It goes to the underlying table to fetch the actual contents.)
Here’s how it works: the runs table on the left refers to row numbers in the underlying table on the right:
There are several helpful properties we can define. I’ll refer to the “unique” object on the left, and the “table” on the right.
These properties are visible from the outside, and they assume that “table” is sorted:
unique.row(0) == table.row(0) unique.count() <= table.count() unique.count() == Set(table.rows()).count for 0 < i < unique.count(): unique.row(i) > unique.row(i-1)
These internal properties are defined in terms of the runs[] table. I’ll sometimes create a test-only “invariant()” method to check internal properties.
if runs.count > 0: runs[0] = 0 for i > 0: table.row(runs[i]) ≠ table.row(runs[i] - 1) for i > 0: table.row(runs[i]) > table.row(runs[i-1]) for i < runs.count - 1: count(i) = runs[i+1] - runs[i] count(runs.count - 1) = table.count() - runs[count-1]
Looking at the last property – it would have been easy to get that wrong.
Can we avoid handling the “end” specially? Yes: add a sentinel value to the runs table. The new last row will have the value table.count(), but we’ll have to be careful that unique.count() not include it. (Then we can delete the last invariant, and use “for i < runs.count: count(i) = runs[i+1] - runs[i]“.
Conclusion
To test list-like objects:
- Consider sufficient completeness: how accessors work with constructor and modifier combinations.
- Handle empty lists.
- Consider what’s special about the beginning, middle, and end of a list.
- Consider the properties that must hold.
- Bonus: consider whether a sentinel value can simplify things.
References
“Programming: Using What’s Hidden“, by Bill Wake. Retrieved 2021-02-07.
“Sufficient Completeness and TDD“, by Bill Wake. Retrieved 2021-02-07.