Immutability is the idea that once created, data never changes. Why might we want this?
- Avoid aliasing bugs: Aliasing occurs when there are multiple ways to access the same piece of data, and one piece changes it in a way the other doesn’t expect.
- Multiple threads can safely share immutable data with less overhead.
- Some structures are stored on “write-once, read-many” data, where you can’t update data you’ve already written.
I mentioned immutability in an earlier article about a two-stack queue algorithm. (See References.) Today I want to explore immutability a bit more.
Data Structures as Values
In many languages, small types such as characters or integers are treated as values, and larger values are managed as references. A value represents itself – the constant 1 doesn’t change if you add 2 to it. A reference is (underneath) a pointer to allocated memory – and the memory it points to can change.
In many functional languages, even complex data structures are treated as values. When you add to or otherwise modify a data structure, you get back a new value.
In Code
Let’s take a stack and compare two possible interfaces. Here’s one that uses a reference to changeable memory – a classic object-oriented approach:
class Stack {
static Stack new()
void push(int i)
void pop()
int top()
bool isEmpty()
}
You use it like this:
s = Stack.new() s.push(42) s.push(17) int i = s.top() s.pop()
Here’s a stack in a “value” style:
class Stack {
static Stack new()
Stack push(int i)
Stack pop()
int top()
bool isEmpty()
}
You can’t tell from the interface description alone, but this is not a single stack that’s being modified. The push() and pop() return (references to) different instances.
Here’s an example of use:
s = Stack.new()
.push(42)
.push(17)
t = s.top()
s2 = s.pop()
We can see that the stacks are different values:
s = Stack.new() s2 = s.push(17) s.isEmpty() // true
Implementation
There’s a simple implementation that can often be used: “modifier” methods return a structure holding the arguments (including references to earlier values), or refer directly to an earlier value. (You can of course use any data structure that supports the semantics.)
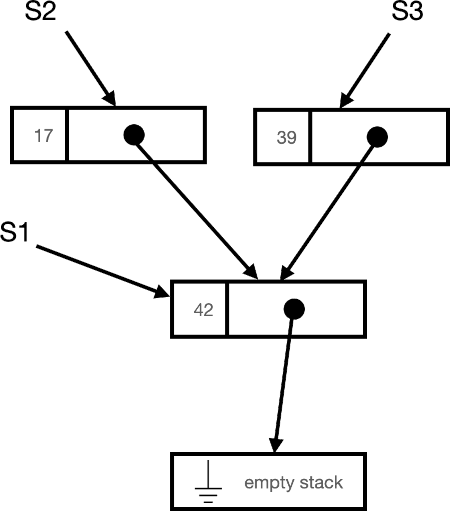
For a linear structure like our stack, we might make the result of push() be a record like this:
The initial stack may be an EmptyStack instance that always returns true for isEmpty().
A series of stacks might look like this:
Thus, push() creates a new record that references an existing stack, and pop() returns an existing stack. There’s no operation that can change an already-created stack.
You can imagine a similar representation for binary trees. You either create a leaf, or make a new node from a value and two leaves, which are stored in a record, structure, or class instance. Again, no operations can change an existing tree.
The “As If” Rule
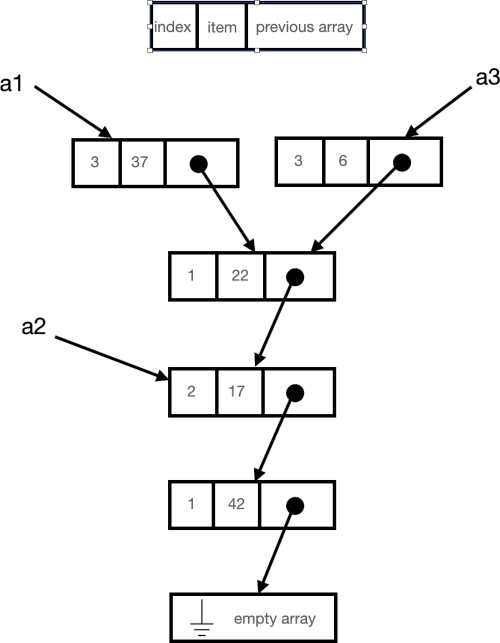
Not every structure is naturally immutable. Consider an array where we can directly address any cell and change it.
If we want that to be immutable, we have to make sure any assignment appears to return a new array. But if we use the implementation described above, we get something like this:
If you’re used to in-memory arrays, this implementation seems horrible. It takes a lot more space, since each assignment allocates multiple fields. Access time is even worse: instead of O(1) direct access, we have to search down a chains of updates.
Another approach is to just copy the array every time it changes. This makes access cheap and updating expensive.
It may surprise you to learn that Swift, a fairly new language, passes arrays by value, so passing an array to a method copies the array.
Actually, that’s not quite true: it passes the arrays “as if” copied.
“As if” means a compiler can use any clever technique it wants as long as the user can’t tell the difference. And there are several choices:
- For a small array, it may be easiest to just copy it.
- If the called method (and methods it calls directly or indirectly) never changes the array, you could pass it by reference.
- Alternately, if the called method could change the array, you can use a “copy-on-write” strategy: any attempt to write triggers a copy, which the callee is free to change. (As I understand it, this is the current Swift strategy.)
- The compiler could do a variation on the method described earlier: accumulate overrides on the base array.
- The code could build a complicated structure that uses slices pointing to the original array, and to the parts that are changed.
- Or, … who knows?
With “as if”, the compiler implementors can do their best job at making tradeoffs, provided they retain the safer semantics.
What’s the Cost?
Immutable types provide gains, at a cost.
One cost is compiler complexity. For example, copy-on-write is a lot harder to manage than C’s “base + size * index” addressing.
Another cost is performance: even if we find ways to mitigate costs in some cases, there may be data types for which we can’t find a solution as performant as the unsafe mutable version.
Consider the queue algorithm I described: it has an amortized (average) cost of O(1) to add or remove items. But an array version can be O(1) for each add or remove. In real-time programs, we might not be willing to tolerate the pause that the two-stack queue causes.
Garbage collectors went through this cycle as well. “Stop the world” garbage collectors found early use, while good real-time collectors took years to develop.
The research community is trying to overcome these overheads. The best explanation I’ve seen is Okasaki’s book (see References), but that’s 20+ years old.
Conclusion
Immutable objects make programs easier to reason about, and make certain types of bugs impossible.
A straightforward implementation can use objects that refer to earlier versions of a structure, but it may not perform as well as we like. More complicated approaches are… more complicated.
In some cases, we may not know how to make an immutable object as performant as a mutable one. Then we have to balance safety vs. performance.
References
“Immutable object“, at Wikipedia. Retrieved 2021-12-07.
Purely Functional Data Structures, by Chris Okasaki. 1999. (I read this a while ago; I think more would have “stuck” if I’d implemented instead of just reading:)
“Queues from Stacks: Functional Data Types“, Bill Wake. Retrieved 2021-12-07.