See also “The Gerrymander Game – Part 2, TDD“
A few weeks ago, Mike Hill published this tweet: “q: how many ways are there to partition a 5×5 tile square into 5 pieces, each containing 5 orthogonally contiguous tiles?” (https://twitter.com/GeePawHill/status/1377772922132176900).
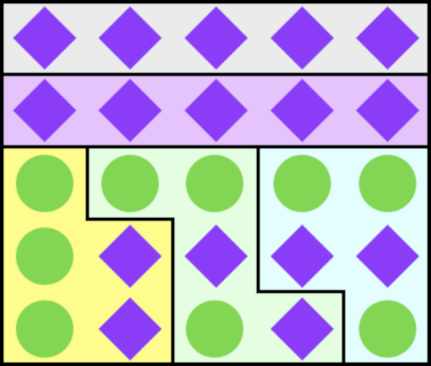
He had in mind a gerrymandering puzzle: Given a 5×5 grid, with 9 green voters & 16 purple voters, it’s pretty clear that purple has the popular vote. But you’re dividing it into precincts of 5 tiles each. Can you lay out the precincts to give the green voters a 3:2 precinct majority?
Sometimes you can:
and sometimes you can’t:
Pentominos?
The constraint on the precincts made me think of pentominos: 5-square shapes, that are connected on a side, never only on a diagonal. (See “Pentomino” in the References.) They’re like the Tetris(™) shapes, but with 5 squares.
In pentomino terms, we want to exactly cover our board with five pentominos. If we can do that, and get the 3:2 precinct majority, we’d be all set.
A search for an existing solution turned up this: the 107 ways to cover the 5×5 grid (https://isomerdesign.com/Pentomino/5×5/index.html).
But looking more closely, this is the 107 ways to do it with no repeated pentominos. It doesn’t include 5 stripes across or 5 stripes down, and we know both those work.
There are 12 basic pentomino shapes. If you treat the ones that have a distinct mirroring as different, there are 18. There are 63 shapes If you count all distinct mirroring and rotations. A five-piece board has 63^5 choices for five pieces (allowing repetition), and this is about a billion. That’s an upper bound, and the true number of 5-piece shapes that will fit is much smaller.
Thus, we have a solution approach: try each possible board covering on the puzzle, and see if you have a solution. If none of the coverings are gerrymandered, it wasn’t possible with that board.
I calculated 4006 unique coverings, but I haven’t had that number confirmed. [Update June 2022: someone else got the same number:)] The good news is it’s a lot smaller than a billion!
I’m a Builder, Not a Solver!
What if you want to build a puzzle for people to solve? You’d like to only give them puzzles that have at least one solution. Since every solution must be a pentomino covering, you can use a tiling to generate many boards.
How many boards are there? Well, a board is a choice of where the 16 purples go (or equivalently, the 9 greens.) Mathematically, this is “25 choose 16”, which is about 2 million. That’s an upper bound, since we know there are unsolvable puzzles included in that. (See above:)
What’s the structure of a good solution? We can start with two precincts of 5 purple (the two precincts purple wins). They call this packing in gerrymandering: if you’re going to lose a district, lose it big. (See “Gerrymandering” in References.)
Now you have 9 green and 6 purple left. Each one has to be a win for green for it to gerrymander. If we divide evenly, we split up the purple votes (cracking), and each remaining district becomes 3 green and 2 purple.
In a sense, this is the only solution: if we traded any purple from one precinct with any green from another, we’d create another precinct majority for purple, and lose the gerrymander.
Thus, any solvable board must be able to have two pentominos completely of the majority color, and three pentominos where the minority color wins.
How Many Puzzles?
Given a pentomino covering, we’d like to create a puzzle from it.
Each board can generate many puzzles. The key bit of math is that “5 choose 2” = 10 – there are 10 ways to choose two items from a set of five.
For each board, make four choices, one of:
10 ways to choose which two of the five pentominos are all purple
* 10 ways to choose which two squares of the first 3-2 pentomino are purple
* 10 ways to choose which two squares of the second 3-2 pentomino are purple
* 10 ways to choose which two squares of the third 3-2 pentomino are purple
= 10,000 ways to color any solution board.
If I’m right that there are 4006 unique solutions, that tells us there are 40,060,000 boards that arise from them. Since there are at most 2M possible boards, we know this full set includes cases where multiple pentomino coverings can solve a given board!
Do you know the pigeonhole principle? (See References.) If you have n+1 pigeons put in n pigeonholes, then at least one pigeonhole has at least two pigeons. And if you have 40M pigeons in 2M pigeonholes, at least one will have 20 pigeons. In other words, there’s at least one board with twenty or more solutions. It would be interesting to know how rare or common that is.
Bottom line: To build a solvable puzzle, take a valid covering and randomly pick one of the 10K ways to color it. To check a solved puzzle, check that its precincts meet the criteria, not that it has the exact covering that generated it.
You Try!
This is a nice-sized problem for test-driven development, and there are several things you could explore:
- The possible pentominos for a given board
- Generating possible tilings
- How to convert a tiling to a game
- Playing and scoring the game
In part 2, I’ll share some of my (partial) solution.
References
“Gerrymandering”, in Wikipedia. Retrieved 2021-04-14.
“The Gerrymander Game – Part 2, TDD“, by Bill Wake. Retrieved 2021-05-05.
“Pentomino“, by Wikipedia. Retrieved 2021-04-14.
“Pigeonhole principle“, by Wikipedia. Retrieved 2021-04-16.
Acknowledgments
Thanks to Mike Hill for proposing the problem, and to Bryan Beecham, Chet Hendrickson, Mike Hill, and Ron Jeffries for jointly exploring how you might solve it.