State Machines: Part 1, Principles

Posted on by

State machines are a very useful abstraction for behavior, but not everybody has run across them. This tool is useful for programmers, and for anybody else who is trying to create or understand a system.

Why take the trouble to understand some formalism? Because it’s easier to get things right when you use a clear model that fits your problem.

The Series

Contents

Three Examples

Here are three examples where state machines might be used.

  1. A recognizer: We’re processing tokens in a programming language. We’d like to recognize when comments of this style occur so we can strip them out: /* COMMENT */ These comments may contain * or /, but do not nest. (Fun exercise: try it yourself, with a state machine or regular expression, before we show a solution.)
  2. The Yacht Game: In the “Yacht” dice game, you roll multiple times, trying to make poker-style combinations. Each turn consists of rolling 5 dice, then you can choose to roll some of those again (up to a total of three rolls), before selecting a category to score in (such as “4 of a kind”).
  3. A BASIC program: Like assembly language or FORTRAN, BASIC programs allow arbitrary GOTOs. We’d like to translate a program to a structured language that doesn’t allow GOTO.

State Machines Defined

We’ll start with a picture, then describe state machines in more mathematical terms. Here is a picture of a typical state machine:

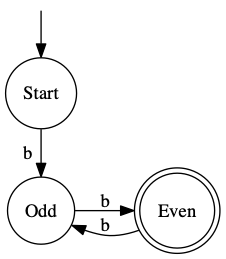
State machine to count odd or even

This machine (a “recognizer”) recognizes strings that have an even number of b’s (not including the empty string.)

A Finite State Machine (FSM) consists of these parts:

  • State: Each state is represented as a bubble. The name in the node is really just for convenience. This machine has 3 states: Start, Odd, and Even.
  • Input Alphabet: These can represent events, characters, etc. In this case, our alphabet has one possibility: “b”.
  • Labeled Arrows: An arrow connects from one state to another (or back to itself), and is labeled by something from the input alphabet.
  • Start State: One node is designated as the starting point, drawn here with an arrow coming from nowhere. Our start state is labeled “Start”.
  • Ending States: One or more nodes is designated as a possible ending point. Typically this is drawn with a double circle. Here, “Even” is the only ending state.

All the above tells us what a state machine looks like, but doesn’t say what it means. In my mental model, you put a checker (a colored disk) on the start state. When an input comes in (from the input alphabet), move the checker along the arrow with that label to the next state. This repeats until the input is done. If the checker finishes in an end state, the input has been valid.

Examples

Example: “b”. The checker starts in Start. It consumes the “b” as input and moves to Odd. We’re done, and not in an end state, so this string doesn’t qualify.

Example: “bbb”. The checker starts in Start, consumes “b” and moves to Odd. It consumes the second “b” and moves to Even. It consumes the third “b” and moves back to Odd. This string also doesn’t qualify.

Example: “bbbb”. The checker goes: Start -> Odd -> Even -> Odd -> Even. We’re in an end state, so the string does meet the criteria.

The picture above is only one way to represent a state machine. Since a state machine is a directed graph (nodes + directed arrows), any graph representation can be the basis of a state machine representation. It’s a “finite” state machine because you have a finite set of states and a finite alphabet.

We’re going to add a restriction for now: deterministic – the arrows coming out of a node must have distinct labels. That is, we can’t use the same input to go to two different states.

A convention: any input that doesn’t correspond to a label goes to an implicit error state (and stays there for any further input).

Another convention: “else” represents the same transition for any inputs not otherwise labeled.

Now try your hand at writing a state machine to recognize /* COMMENTS */!

Application

Let’s go back to the examples we started with:

Yacht Game

The input alphabet is
roll: roll all or selected dice
toggle: set whether a die is in or out of the set of dice to re-roll
choose: select the category for the dice you have showing

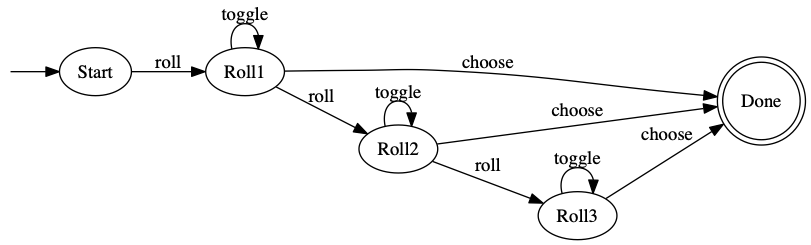
State machine for the Yacht game

BASIC program

Here’s a short unstructured BASIC program to count a’s and b’s:

10 A=0; B=0
15 C=READ()
20 IF C='A' GOTO 30
25 IF C='B' GOTO 40
28 GOTO 50
30 A=A+1; GOTO 15
40 B=B+1; GOTO 15
50 PRINT A, B
55 STOP

And here’s a corresponding state machine:

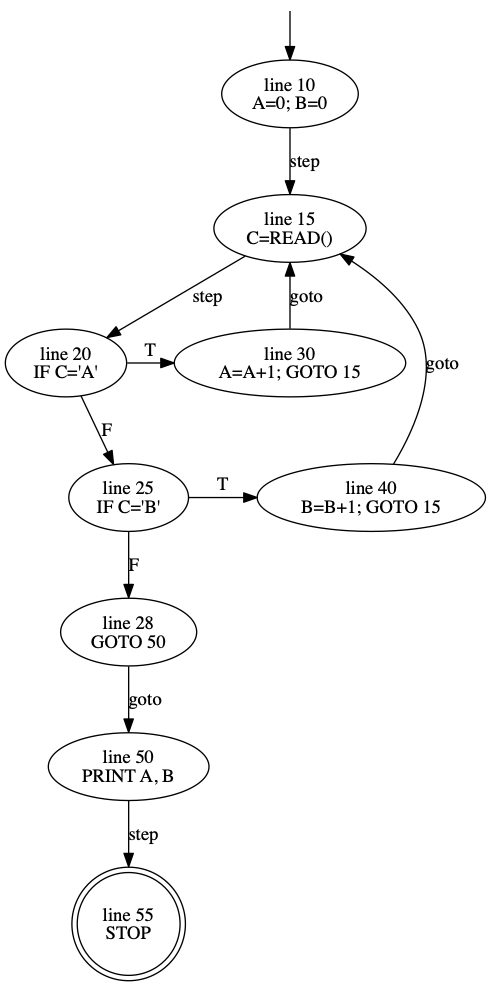
State machine for a BASIC program

Here, I’ve used step to mean it falls through to the next line, goto for a GOTO statement transfer, and T and F for true or false as a result of a conditional.

The state machine doesn’t define a full interpreter, but does show us the control flow.

Comments

Did you try the comments challenge? Here’s some sample input to try against your machine:

/              -- not a comment
/*             -- not a comment
/*/            -- not a comment
/**/           -- valid comment
/* comment */  -- valid comment
/***/          -- valid comment
/* *x/         -- not a comment
/*** x ***/    -- valid comment

How did you do?

Here’s my state machine:

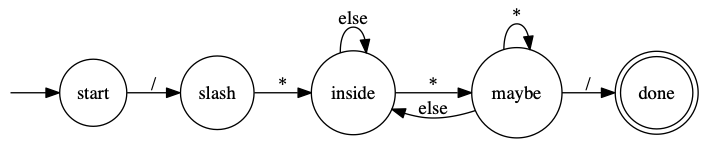
state machine for Pascal-style comments

The tricky part of this is that “maybe” state – we have to recognize that we might have multiple *, or that we might go back to clearly being inside the comment.

Limitations

State machines are handy, but they’re not able to model everything.

The problem is that their only memory is “what state am I in?” It’s the difference between “Where am I?” and “How did I get here?” – the second question is just too hard for them.

For example, you can’t write a state machine to tell if you have properly balanced parentheses. (Try it!) But you can do this if you add a stack.

And you can’t write a state machine that can perform an arbitrary computation, unless you add (potentially infinite:) memory.

This is a foundational result in computation theory: there are classes of computation that can only be performed by more sophisticated mechanisms. See “Chomsky Hierarchy“, “Turing Machines“, or “Pumping Lemma” for more information.

But for Turing machines or CPUs, you’ll still see a state machine hidden inside.

Extensions to State Machines

With such a useful tool, it’s not surprising there are a number of extensions.

Non-Deterministic Finite State Automata (NDFSA)

A deterministic FSA allows only one arrow labeled with something from the input alphabet. A non-deterministic FSA removes that restriction in two ways: 1) more than one arrow can have the same label, and 2) we allow “empty” transitions.

An empty transition is a “freebie” – you can just transition without consuming any input. Show an empty transition in one of two ways: the Greek letter epsilon (ε) for “empty”, or the Greek letter lambda (λ) which I can only assume stands for “La-la-la, loser – you have to memorize a meaningless symbol.”

At any rate, non-determinism complicates the checker model. Now, in effect, you’re in multiple states at once, so you need lots of checkers. You add checkers to cover all the choices, and remove the ones that get blocked.

Non-determinism is handy for writing, even if it’s harder to implement. The crazy thing is – deterministic and non-deterministic FSAs can describe the same sets of sequences. You can convert non-deterministic to deterministic by creating a machine where the deterministic states correspond to sets of states in the non-deterministic machine (but it may have a lot more states).

I’ve seen non-deterministic automata used in compiler descriptions (usually for the grammar of the tokens, not the language itself). Some tools support this. Ken Thompson’s early regular-expression implementation used a non-deterministic FSA directly (see the reference).

Actions on Transition

One common extension is to allow actions to be associated with each arrow. If you traverse an arrow, you take the action. Here’s an example: it recognizes integers, and computes their value. (“d” is assumed to be the current input character as a value 0-9.)

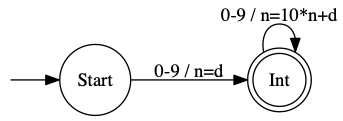
State machine that calculates integers

Actions on State Entry or Exit

Another variant allows you to specify actions when you enter and/or leave a state. Our BASIC program fits that model – imagine the code inside the node being executed, then flow of control being followed.

Even More Variants We Won’t Look At

Some other variants; see the references for more information:

  • Regular Expressions – Finite states machines and regular expressions are equivalent, in that both have the same power – can recognize the same sets of strings. (They have the same limitations too, e.g., neither can tell if an arbitrarily deep set of nested parentheses balances correctly.)
  • UML state diagrams – allow for entry and exit conditions, as well as actions on states or transitions. They also allow hierarchical machines and more.
  • Statecharts – a graphical approach which was an inspiration for many of the UML state diagram features.
  • Petri Nets – a formalism for describing distributed systems. (This is probably where I picked up the notion of using checkers to track which state you’re in.)

Conclusion

State machines (and all their variants) have proven themselves over and over. Learn to read and understand them, and you’ll be a step ahead for many situations that focus on behavior.

Resources