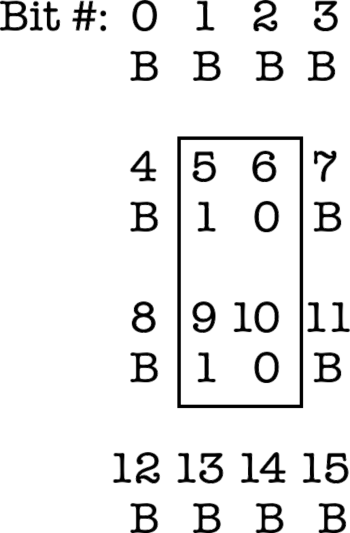The Gerrymander Game – Part 2, TDD

See also “The Gerrymander Game – Part 1, Puzzle“

I implemented the core of the gerrymandering game using TDD, and it was a challenge. Why? Because I didn’t know in advance how to solve it. 

My Overall Strategy

To make the gerrymandering game, I had these four parts (as discussed in Part 1):

• Generate all possible tilings
• Select a tiling to define the precincts
• Generate a puzzle by assigning voters to the precincts
• Let the user try to gerrymander by choosing a tiling

I haven’t yet implemented a user interface to let a user solve the puzzle by making their own tiling.  (Tile generation was the part that got me most interested.)

Representing Pentominos

To tile a board, we know we’ll have to keep track of shapes and their locations.

I remembered that the very first checkers program (written in 1952!) had used a bit string to represent boards, using a few spare bits to represent moves off the edge of the board. (See the checkers article in the References.)

I thought I’d do something similar: put ominos in a rectangle, represented as a bit string. I put a border around them, so I could detect a placement that went “off the edge”.

A 2×2 board would look like this:

The “B” bits might be 0 or 1, depending on the situation. This example represents a vertical bar, with bits 5 and 9 set. If we try to move it up, left, or down, it will intersect the border. However, we can move it safely one to the right. 

If you wrote this out as a bit string, it would look like this:

BBBB_B01B_B01B_BBBB

(Bit 0 is the rightmost bit; bit 15 is the leftmost.)

As I write this, I realize I could have saved a few bits by visualizing the board as wrapped around a cylinder, with only one border bit on the sides instead of two.

From the TDD side, it is unusual for me to worry about representation so early. Partly this was because I was interested in how the bit representation would work; partly I was a little worried that since there might be millions or even billions of these, it would be good to start with a compact representation. (I was using Swift, with a 64-bit unsigned integer.)

Normalized Ominos

To handle the shapes, I started with the 18 basic pentominos, and generated their 63 rotations and permutations. 

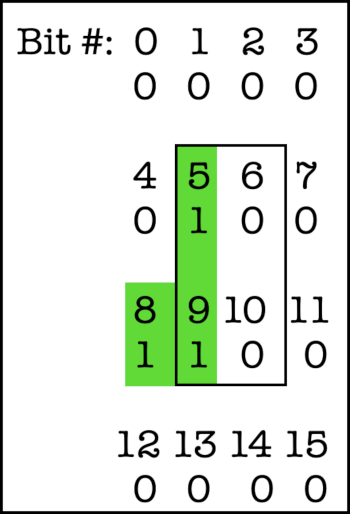
I decided that each shape would be normalized to have its leftmost, top-most bit in row 1, column 1. The border bits would default to 0. Here’s what that looks like for a backwards L: 

Notice that it encroaches the border – as it should, since this piece can’t legitimately be placed there. 

Attempting a Placement

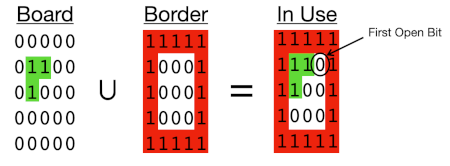
The heart of the placement algorithm takes five steps:

1. Union the board so far with the border.
2. Find the next open position: the topmost, leftmost 0 bit.
3. Move the omino to be placed so that its (1,1) cell is in the open position. 
4. Compute the intersection of the moved omino and the board+border. 
5. Any 1 bits => FAIL. The placement overlaps an existing board item or border.
   Otherwise => SUCCESS. Add the new omino to the board so far.

Let’s see that in pictures. First we’ll find the union of the board and the border: 

Then we’ll take the next omino, and slide it over so its top cell is in the open position. Once that’s there, we’ll intersect it with the “in use” cells. 

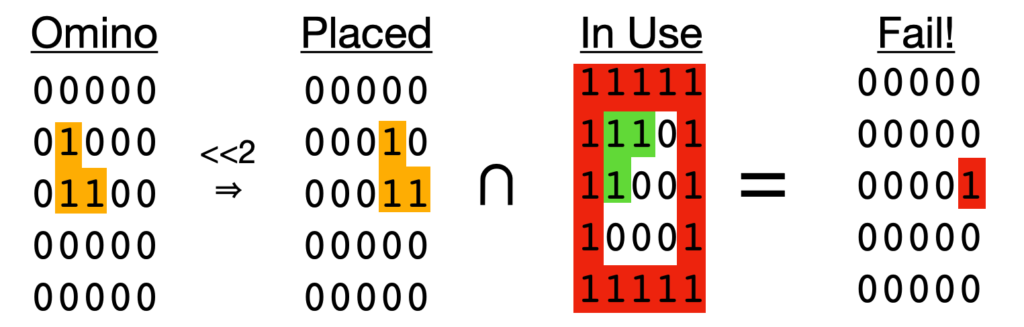
We can see that there is one bit set: our omino intersects the border. Therefore, this placement fails. 

A Backtracking Algorithm

A classical backtracking algorithm builds a tree of possibilities, a little at a time, and explores it in a disciplined way (e.g., a stack or queue). I used an algorithm like that in the Sudoku game I did a while back. (See References.)

I had a different idea for the gerrymandering puzzle. What if we could enumerate all the possible tilings? If you include the unsuccessful ones, there are too many. But it could work if we could skip past the bad ones. (Once a bad move is made, there’s no point trying to tile the rest!)

I envisioned something like an odometer where the digits are on a wheel and you see one of them: 

But instead of digits, it would have pentominos: 

For our full problem, we have 63 pentominos per “wheel”, and 5 wheels, so about a billion possible combinations. 

So we don’t have to look at all of them, we’re going to take this approach:

• Position one wheel at a time
• Try the current wheel’s pentomino in the next open space.
• No overlaps with the “board U border”? Move on to the next wheel, starting with its first pentomino.
• There are overlaps? Try the next pentomino on the current wheel. If it’s at the end, go left a wheel and try its next pentomino.

If you reach the right edge, you’ve got a successful tiling. Record it, and continue spinning the wheels. 

If you hit the left edge, you’ve tried all the variations, and you’re done. 

TDD – Shape/Omino

To implement all this with TDD, I mostly used a monomino (one cell) and triominos (three) to create examples, then used five cells at the end to see the results for the full problem. 

I usually try to drive examples from the problem’s essence, but in this case I jumped down a level, starting with a Shape class that dealt with the bits and the positions. I wanted to make sure my intuition about having a border was useful. 

At some point, I had Ominos that contained Shapes, but I folded them all together to one class: Omino.

The bit arithmetic worked as I’d hoped. The core computation boils down to:

(board | border) & (candidate << distance) == 0

although I don’t have it as clearly as that. Maybe I should.

Mistakes with Shapes

I made several mistakes along the way:

1. Positions. I had defined an At class to represent coordinates. It was just a data bag with x and y. But I kept thinking “row, column”, and using At that way. At some point, the IDE popped up x and y as suggested arguments, and it finally dawned on me that I was using it inconsistently:)

2. Bits. Bits are numbered from 0 to 63 (with UInt64), right to left. But my board was intended to be laid out left to right as shown above. That was confusing as the ominos got more interesting. I invested in a factory method that took strings like this: “x..|x..|x..” for the vertical bar. I could visualize that a lot better than the backward bit strings. But I still was able to use “>>” rather than “<<”. 

3. Off-By-One. The border changes the size from nXn to (n+2)X(n+2). The first border position is at row 0, column 0; the first omino position is at row 1, column 1. I’m so used to 0-based counting that it was easy to forget I needed to do 1-based sometimes. 

4. Board size. At some point, I had to start keeping track of the size of the shapes. I resisted adding a count to the class for too long, passing the count around as a parameter. I eventually added it to omino, but some methods still have the parameter. 

TDD – Odometer/Combinations

The Odometer was challenging. It originally started out as a Board. 

I did a very unusual “Sketch in Code” move; you might even say it wasn’t a TDD move at all. I had the core idea for the algorithm in my head, and I typed it in. After staring at it for a while, I deleted it (without running tests or even compiling). I did this three times in a row, then used TDD as I normally would.

It helped just to see the parts together in one place.

I changed the name from “Odometer” to “Combinations”, having in mind a wheel-style combination lock:

A friend once had a cheap bike lock version: you could pull on it as you spun the wheel, and figure out the digits one at a time. The backtracking algorithm works similarly.

The Combinations object represented a lock with multiple acceptable combinations. 

At first, that object maintained three structures: the shapes placed so far, where they were put, and the resulting board. Now, I only track where the shapes are put, and take a snapshot of the wheels when I want to remember a tiling. 

Here are Combination’s methods:

func moveDown()        // go to next position of current wheel
func moveRight()       // go to next wheel
func moveLeft()        // go back to previous wheel

func isDone() -> Bool // out of combinations to try
func isSuccessful() -> Bool    // tiling succeeded

func value() -> Int      // the current wheel’s position
func placeAt(_ at: At)   // remember the placement
func tiling(_ ominos: [Omino]) -> Tiling  // snapshot

Moving out the placeAt() and tiling() methods would yield a more general backtracking algorithm. 

Limitations and Future Directions

The code right now assumes it’s dealing with nxn square boards, and only size n ominos. The algorithm would work with other shapes or sizes, but at some point large sizes would overwhelm it.

In particular, UInt64 is limited to 6×6 boards (plus border). You could manage an array of UInt64s, but as the sizes grow, the number of empty bits grows even faster. That suggests a sparse representation might pay off better for large problems. (And there are other approaches too:)

The tiling is relatively slow – about 60 seconds to find 4006 tilings from the ~1 billion possibilities. To support a real game, that’s not an issue, as you could generate them in advance and quickly generate puzzle boards from them. 

I’ve got code to generate and display a game board, but I don’t have an interactive user interface for the game itself. I’ve got some ideas…

Conclusion

The Gerrymandering Game has brought together several areas:

• The political science aspect of gerrymandering itself.
• The mathematical side of tiling a space, and pentominos in particular.
• Software issues around representation of space, generating combinations, and backtracking. 
• TDD issues around avoiding classic errors (such as off-by-1), and around creating unfamiliar solutions.

It’s been a fun project so far!

References

“Some Studies in Machine Learning Using the Game of Checkers”, by A.L. Samuel, in Computers and Thought, 1963, edited by Feigenbaum and Feldman. (2012 reissue)

“Sudoku Solver”, by Bill Wake. https://xp123.com/articles/sudoku-solver/ 

“The Gerrymander Game – Part 1, Puzzle”, by Bill Wake. https://xp123.com/articles/gerrymander-game/

Acknowledgments

Thanks again to Mike Hill for introducing me to the problem, and Bryan Beecham, Chet Hendrickson, Mike Hill, and Ron Jeffries for discussing the problem and my solution.