And-Or Trees

Suppose you want to represent a finite set of possibilities in a compact way. An And-Or Tree can do this, and is useful in several situations.

An And-Or Tree has leaf nodes and interior nodes. The leaf nodes contain some sort of information. The interior nodes are either “and” or “or”. Those contain children each of which is an And-Or Tree.

There are several variations. In some forms, you can have groups of “and” and “or” at the same level. Some require that “and” and “or” alternate levels. Some allow information to be attached to interior nodes as well. We’ll take the traditional math approach and leave the variations as exercises for the reader.

And-Or Trees In Code

One way to write these is as a straightforward translation of the definition. I’m using Swift, so I can use its wonderful indirect enum (“sum”) type. In Java and similar languages, you could use classes and inheritance in a Composite pattern.

indirect enum Tree<INFO> {
  case leaf(INFO)
  case or([Tree])
  case and([Tree])
}

The three cases of an enum come with attached information specific to that case. The indirect keyword indicates that this is a recursive type.

Uses

We’ll look at several applications for this structure.

1. Regular Expressions for Finite Languages

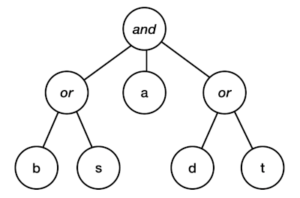
A language is a set of strings. If the set is finite, an And-Or Tree can easily represent it. “And” corresponds to concatenation; “Or” corresponds to alternation. Since the set is finite, there is no (Kleene) star to allow repetition.

For example, the set {bad, sad, bat, sat} could be represented as a tree in several ways, but here’s a useful one, minimal in some sense.

2. Search Tree (in Games)

Consider a system that plays chess or some other turn-based game. Upcoming moves form a tree of possibilities – move and response, move and response. These trees may be finite, but they often have a huge number of possibilities and can’t be searched exhaustively.

The “and” and “or” reflect that you have to treat your moves and your opponent’s responses differently: you pick one move for yourself (“or”), but you have to consider all your opponent’s possible responses (“and”).

A basic search looks through a fixed number of levels; more sophisticated approaches might dive deeper when it’s hard to judge.

3. Circuits with AND and OR Gates

For circuits, the leaf nodes represent inputs (or their negations), and “and” and “or” are two different typers of circuits.

A typical challenge might be: given an arbitrary tree, convert it to a three-level tree, a disjunction (“or”) of conjunctions (“and”) of inputs. This reduced form can represent an efficient circuit, minimizing the number of gates.

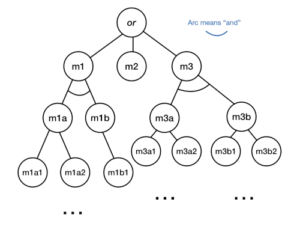
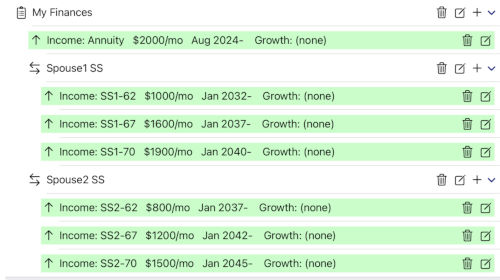
4. Compact Representation of Scenarios

This is the case I’m working on: I’m devising a planner that lets you describe pools or streams of money, contained in groups (“and”) or scenarios (“or”).

For example:

This describes 1 * 3 * 3 = 9 alternatives.

We generate each possible scenario and compute its net worth, so you can choose among alternatives.

Algorithm to Walk an And-Or Tree

Let’s look at an algorithm for generating the possibilities. You could use this with the (finite) regex to generate all possible strings, or in our planner to generate possible scenarios. In this case, we’ll generate strings from a (restricted) regular expression.

We have to generate combinations of items, so let’s start with a function for that:

func combinations<T, U>(_ xs: [T], _ ys: [T], _ fn: (T, T) -> U) -> [U] {
  var result = [U]()
  xs.forEach { x in
    ys.forEach { y in
      result.append(fn(x, y))
    }
  }
  return result
}

It’s a little abstract because it’s generic, but it takes two arrays, generates the combinations of all their elements (any element of the first array with any element of the second), and runs a function to combine each pair into a single value.

The next function is on the enum, and generates the list of all possible strings.

  func generate() -> [String] {
    switch self {
    case .leaf(let string):
      return [string]

    case .or(let children):
      return children
        .map { $0.generate() }
        .flatMap { $0 }

    case .and(let children):
      return children
        .map { $0.generate() }
        .reduce([""]) { partial, child in
          combinations(partial, child, +)
        }
    }
  }
}

This is pretty dense. But it basically takes the three cases in our enum:

1. A leaf contains a single string, so it returns an array with just that string.
   
2. An “or” has a set of alternatives. The map() turns each child into an array of its possible values, and the flatMap() turns [[String]] into [String].
   
3. The “and” is the most complicated. It starts by mapping each child to its list of possibilities, as the “or” did. But then it needs to build the possible combinations of concatenations: each possible string from its first child to each possible string from its second child, and so on, until all are concatenated.

Reduce() is a function to do that. It takes a starting value, [""], and passes that to the closure as the partial, along with the next child from the list. We generate each possible value from the child, then combine it with the previous partial to get the partial value that goes with the next child.

If we had picked [] for our starting value, it wouldn’t have worked: the combinations of an empty list with any array is an empty array.

If you haven’t seen map() or reduce() before, they are worth learning. Map() turns a sequence of one object into a sequence of another; reduce() combines multiple objects in a sequence to a single value. The map-reduce pair is very powerful.

Conclusion

The And-Or Tree is a little deep in my bag of tricks, but it’s handy for things that map to finite regular languages. Let me know if you find a use for it!

References

“And-or tree”, Wikipedia. https://en.wikipedia.org/wiki/And–or_tree Retrieved 2024-08-19.

“Tree-Like Objects – TDD Patterns“, by Bill Wake. https://xp123.com/tree-like-objects-tdd-patterns/. Retrieved 2024-08-19.